The Inscribed Square Problem: Unraveling Mathematical Mysteries

- Authors
- Published on
- Published on
In the thrilling world of mathematics, there exists a mind-boggling conundrum known as the inscribed square problem. First introduced by the legendary Otto Toeplitz back in the day, this puzzle challenges the very essence of closed continuous loops. The burning question on everyone's mind is whether every single one of these loops out there harbors an inscribed square within its squiggly confines. And let me tell you, folks, this is no ordinary brain teaser. It's the stuff that keeps mathematicians up at night, pondering the mysteries of geometry and topology.
Now, fast forward to a simpler version of this enigma, where we delve into the realm of inscribed rectangles. Enter Herbert Vaughan, the mastermind behind a beautiful proof that sheds light on this intricate problem. As we embark on this mathematical journey, we find ourselves face to face with the elusive Klein bottle, not just a quirky oddity but a powerful tool for cracking the code of inscribed shapes. It's a second edition of mathematical exploration, brimming with new research and fascinating connections that will leave you spellbound.
But why should we care about proving the existence of inscribed rectangles in closed loops, you may ask? Well, my dear viewers, engaging with such challenging puzzles isn't just about solving abstract problems. It's about honing our problem-solving instincts, sharpening our minds for practical applications down the road. And let me tell you, there's nothing quite like the thrill of unraveling the secrets of topology, where bizarre shapes and mind-bending properties transform into powerful tools for logic and deduction. So buckle up, ladies and gentlemen, as we dive deep into the world of inscribed shapes and embark on a mathematical adventure like no other.

Image copyright Youtube
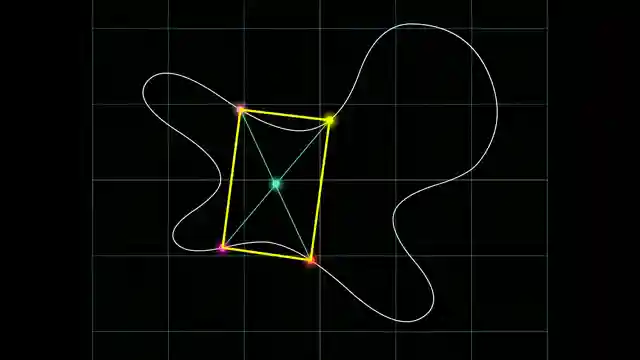
Image copyright Youtube

Image copyright Youtube
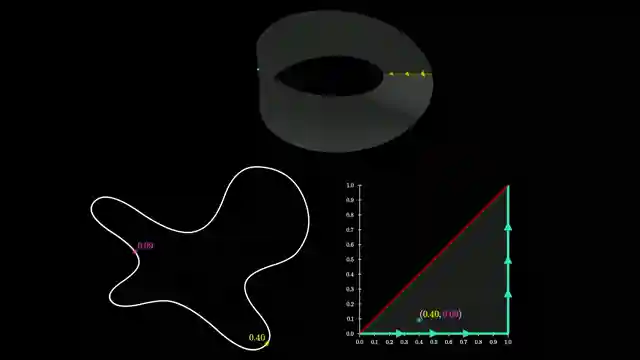
Image copyright Youtube
Watch This open problem taught me what topology is on Youtube
Viewer Reactions for This open problem taught me what topology is
Viewer had a realization about topology after watching the video
Practical application of topology in a conference paper
Appreciation for the educational content and animations in the video
Request for 3D versions of videos for better visualization
Insights into topology concepts and their applications
Comparison between algebraic topology and topology as different branches of math
Personal experiences and connections to the video's content
Praise for the video's teaching style and problem-solving approach
Comments on the beauty and complexity of mathematics demonstrated in the video
Humorous comments and references to the content of the video
Related Articles
Decoding Grover's Algorithm: Quantum Computing Demystified
Explore Grover's algorithm and quantum computing concepts clarified by 3Blue1Brown. Learn about translating classical verifier functions, state vectors, and linear transformations in this insightful breakdown.

Unveiling Quantum Computing: Grover's Algorithm Demystified
Explore quantum computing misconceptions and the groundbreaking Grover's algorithm. Learn about state vectors and probabilistic distributions in this illuminating 3Blue1Brown video.

Unlocking Pi: Colliding Blocks, Quantum Computing, and Conservation Principles
Explore the captivating world of computing pi with colliding blocks in this Pi Day special by 3Blue1Brown. Discover the connection to quantum computing, conservation principles, and the intriguing parallels to Grover's Algorithm. A thrilling journey into physics and problem-solving awaits!

Unveiling Cosmic Distances: A Journey with 3Blue1Brown and Terrence Tao
Explore the fascinating history of measuring cosmic distances from parallax to Venus transits. Witness groundbreaking discoveries and astronomical milestones in this cosmic journey with 3Blue1Brown and Terrence Tao.
