Mastering Math Puzzles: Higher Dimensions & Geometric Challenges

- Authors
- Published on
- Published on
Today, the lads at 3Blue1Brown have cooked up a series of mind-bending puzzles that'll have your brain doing more laps than a Formula 1 race. First up, they're diving headfirst into the world of higher dimensions, starting with a hexagon tiling extravaganza. Imagine rotating hexagons like a Rubik's cube on steroids to create new patterns - it's like a geometric dance that'll leave you dizzy with excitement. But hold onto your helmets because the real challenge lies in figuring out the maximum number of moves needed to shift from one mind-bending pattern to another. It's a puzzle so complex, it'll make your head spin faster than a Bugatti Veyron.
Next on the agenda is the Tarski-Planck problem - a mathematical conundrum that'll have you scratching your head like a confused chimpanzee. Picture covering a circle with strips like a giant mathematical pie, and the question is, can you do it in a way that minimizes the sum of widths? It's a race against the clock to crack the code and find the most efficient strip strategy. And just when you thought things couldn't get any wilder, the lads throw in a curveball with the intersection of external tangents to three circles. Strap in, because this puzzle will have you navigating through a mathematical maze that's trickier than a rally stage in the Amazon rainforest.
But fear not, because the lads at 3Blue1Brown have a trick up their sleeve - a leap into the third dimension. By projecting circles onto spheres and visualizing external tangents as cones, they unveil a whole new perspective that'll have you seeing math in a way you never thought possible. It's like taking a rollercoaster ride through a mathematical wonderland, where every twist and turn reveals a new layer of complexity. So buckle up, because this mathematical journey is about to take you on a ride of a lifetime, where the only limit is your imagination.
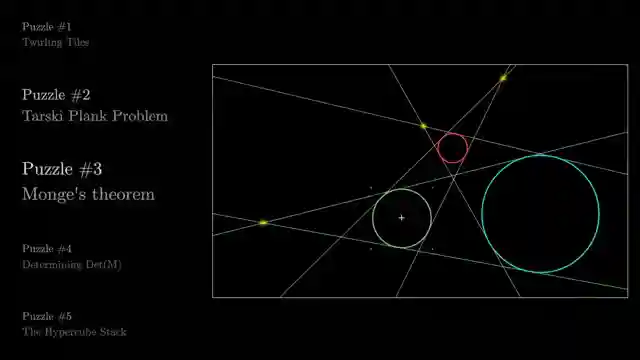
Image copyright Youtube

Image copyright Youtube
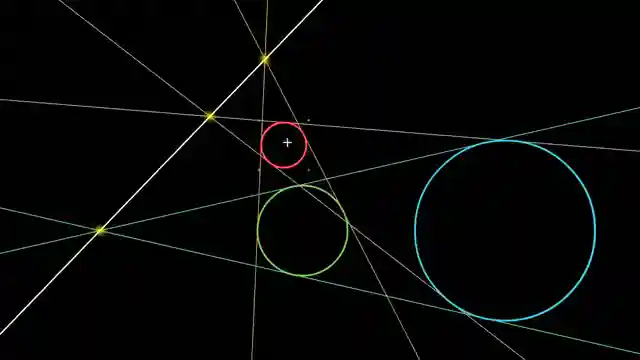
Image copyright Youtube
Image copyright Youtube
Watch Why 4d geometry makes me sad on Youtube
Viewer Reactions for Why 4d geometry makes me sad
Viewers appreciated the video for its thought-provoking content and captivating visuals
Some viewers shared their experiences with visualizing 4D shapes and the challenges of understanding higher dimensions
Mention of using Monge's Theorem in practical applications like building laser pointing systems
Comments on the uniqueness and difficulty of comprehending 4D structures
Appreciation for the channel's ability to make abstract concepts intuitive and accessible
Discussion on the special nature of dimension 4 and its relevance in various phenomena
Some viewers shared personal anecdotes related to math and problem-solving
Comments on the difficulty of grasping 4D structures due to graphing in lower dimensions
Mention of the video's animations being impressive and captivating
Some viewers shared their interpretations of the visual puzzles presented in the video
Related Articles
Decoding Grover's Algorithm: Quantum Computing Demystified
Explore Grover's algorithm and quantum computing concepts clarified by 3Blue1Brown. Learn about translating classical verifier functions, state vectors, and linear transformations in this insightful breakdown.

Unveiling Quantum Computing: Grover's Algorithm Demystified
Explore quantum computing misconceptions and the groundbreaking Grover's algorithm. Learn about state vectors and probabilistic distributions in this illuminating 3Blue1Brown video.

Unlocking Pi: Colliding Blocks, Quantum Computing, and Conservation Principles
Explore the captivating world of computing pi with colliding blocks in this Pi Day special by 3Blue1Brown. Discover the connection to quantum computing, conservation principles, and the intriguing parallels to Grover's Algorithm. A thrilling journey into physics and problem-solving awaits!

Unveiling Cosmic Distances: A Journey with 3Blue1Brown and Terrence Tao
Explore the fascinating history of measuring cosmic distances from parallax to Venus transits. Witness groundbreaking discoveries and astronomical milestones in this cosmic journey with 3Blue1Brown and Terrence Tao.
