Unraveling the Mystery: Finding Shortest Paths on Cartesian Plane

- Authors
- Published on
- Published on
In this thrilling episode, the Computerphile team takes us on a wild ride through the perplexing world of finding the shortest path in a graph on a Cartesian plane. It's like trying to navigate a maze with only two possible routes, a real head-scratcher that even the most seasoned algorithm enthusiasts find baffling. They draw parallels to the SAT problem, where constraints must be met, adding an extra layer of complexity to the already mind-boggling task at hand.
As they delve into the nitty-gritty of calculating path lengths using Pythagoras's theorem, the team uncovers the challenges posed by irrational numbers and the need for precision in summing square roots. It's a high-stakes game of mathematical precision, where even the slightest miscalculation could throw off the entire journey. The team humorously navigates through the intricacies of determining which sum of square roots reigns supreme, showcasing the fine line between simplicity and complexity in algorithmic analysis.
Despite the practical ease of algorithms like Dijkstra's in finding shortest paths efficiently, the team sheds light on the underlying complexity of algorithmic analysis. It's a rollercoaster of a revelation, where what seems straightforward on the surface turns out to be a Herculean task under the hood. Through their witty banter and insightful exploration, the Computerphile team leaves us pondering the enigmatic nature of seemingly simple problems and the intricate web of challenges that lie beneath.

Image copyright Youtube

Image copyright Youtube
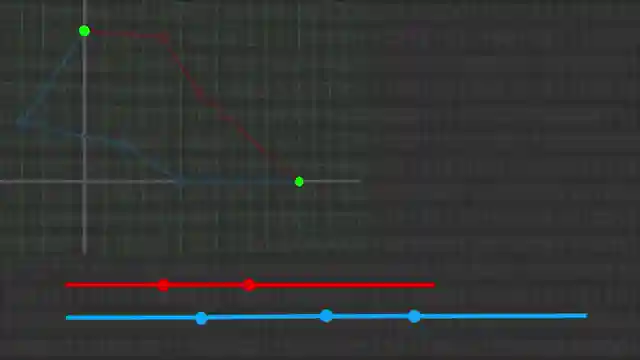
Image copyright Youtube

Image copyright Youtube
Watch Shortest Path Algorithm Problem - Computerphile on Youtube
Viewer Reactions for Shortest Path Algorithm Problem - Computerphile
Math guy finds problem very hard, engineer sees paths as same length
Pathfinding angle is a red herring
Discussion on practical vs. theoretical impossibility
Comparing squared distances for determining longer vector
Exploring different methods for solving the problem without square roots
Speculation on exploiting difficulty for cryptography
Suggestions to skip square roots and compare sum of squares
Comments on accent and pronunciation
Suggestions to avoid square roots in calculations
Discussion on the redundancy of square roots in finding shortest path
Related Articles

Unleashing Super Intelligence: The Acceleration of AI Automation
Join Computerphile in exploring the race towards super intelligence by OpenAI and Enthropic. Discover the potential for AI automation to revolutionize research processes, leading to a 200-fold increase in speed. The future of AI is fast approaching - buckle up for the ride!

Mastering CPU Communication: Interrupts and Operating Systems
Discover how the CPU communicates with external devices like keyboards and floppy disks, exploring the concept of interrupts and the role of operating systems in managing these interactions. Learn about efficient data exchange mechanisms and the impact on user experience in this insightful Computerphile video.

Mastering Decision-Making: Monte Carlo & Tree Algorithms in Robotics
Explore decision-making in uncertain environments with Monte Carlo research and tree search algorithms. Learn how sample-based methods revolutionize real-world applications, enhancing efficiency and adaptability in robotics and AI.

Exploring AI Video Creation: AI Mike Pound in Diverse Scenarios
Computerphile pioneers AI video creation using open-source tools like Flux and T5 TTS to generate lifelike content featuring AI Mike Pound. The team showcases the potential and limitations of AI technology in content creation, raising ethical considerations. Explore the AI-generated images and videos of Mike Pound in various scenarios.
